An inverted interval is one that is turned upside down, either by raising the lower note an octave (and placing it on top) or by lowering the upper note an octave (and placing it on the bottom).
When we invert an interval, we create a new interval, measured by the major scale of the (new) lower note.
This post will take us through the process of inverting diatonic (perfect and major) and altered (minor, diminished and augmented) intervals, and provide instruction on how to measure the inverted interval.
Examples of how to play the intervals on a guitar are provided in Intervals I and II.
Inverted Perfect Intervals
Perfect Fourths
When we invert a perfect fourth interval, it becomes a perfect fifth interval.
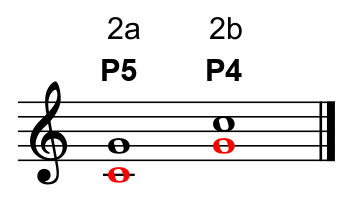
The distance between a C (the first note in a C major scale) and an F (the fourth note) is a perfect fourth (fig.1a).
When we raise the C an octave and place it above the F, we have inverted the interval and created a new one, measured from F to C (fig.1b).
The distance between an F (the first note in an F major scale) and a C (the fifth note) is a perfect fifth.
Fig.1

Perfect Fifths
When we invert a perfect fifth interval, it becomes a perfect fourth interval.
The distance between a C (the first note in a C major scale) and a G (the fifth note) is a perfect fifth (fig.2a).
When we raise the C an octave and place it above the G, we have inverted the interval and created a new one, measured from G to C (fig.2b).
The distance between a G (the first note in a G major scale) and a C (the fourth note) is a perfect fourth.
Fig.2
Inverted Major Intervals
Major Seconds
When we invert a major second interval, it becomes a minor seventh interval.
The distance between a C (the first note in a C major scale) and a D (the second note) is a major second (fig.3a).
When we raise the C an octave and place it above the D, we have inverted the interval and created a new one, measured from D to C (fig.3b).
The distance between a D (the first note in a D major scale) and a C (the flatted seventh note) is a minor seventh.
Fig.3

Major Thirds
When we invert a major third interval, it becomes a minor sixth interval.
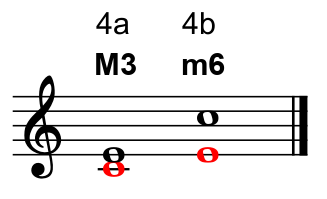
The distance between a C (the first note in a C major scale) and an E (the third note) is a major third (fig.4a).
When we raise the C an octave and place it above the E, we have inverted the interval and created a new one, measured from E to C (fig.4b).
The distance between an E (the first note in an E major scale) and a C (the flatted sixth note) is a minor sixth.
Fig.4
Major Sixths
When we invert a major sixth interval, it becomes a minor third interval.
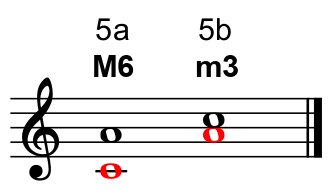
The distance between a C (the first note in a C major scale) and an A (the sixth note) is a major sixth (fig.5a).
When we raise the C an octave and place it above the A, we have inverted the interval and created a new one, measured from A to C (fig.5b).
The distance between an A (the first note in an A major scale) and a C (the flatted third note) is a minor third.
Fig.5
Major Sevenths
When we invert a major seventh interval, it becomes a minor second interval.
The distance between a C (the first note in a C major scale) and a B (the seventh note) is a major seventh (fig.6a).
When we raise the C an octave and place it above the B, we have inverted the interval and created a new one, measured from B to C (fig.6b).
The distance between a B (the first note in a B major scale) and a C (the flatted second note) is a minor second.
Fig.6

Inverted Minor Intervals
Minor Seconds
When we invert a minor second interval, it becomes a major seventh interval.
The distance between a C (the first note in a C major scale) and a Db (the flatted second note) is a minor second (fig.7a).
When we raise the C an octave and place it above the Db, we have inverted the interval and created a new one, measured from Db to C (fig.7b).
The distance between a Db (the first note in a Db major scale) and a C (the seventh note) is a major seventh.
Fig.7

Minor Thirds
When we invert a minor third interval, it becomes a major sixth interval.
The distance between a C (the first note in a C major scale) and an Eb (the flatted third note) is a minor third (fig.8a).
When we raise the C an octave and place it above the Eb, we have inverted the interval and created a new one, measured from Eb to C (fig.8b).
The distance between an Eb (the first note in an Eb major scale) and a C (the sixth note) is a major sixth.
Fig.8

Minor Sixths
When we invert a minor sixth interval, it becomes a major third interval.
The distance between a C (the first note in a C major scale) and an Ab (the flatted sixth note) is a minor sixth (fig.9a).
When we raise the C an octave and place it above the Ab, we have inverted the interval and created a new one, measured from Ab to C (fig.9b).
The distance between an Ab (the first note in an Ab major scale) and a C (the third note) is a major third (fig.9b).
Fig.9

Minor Sevenths
When we invert a minor seventh interval, it becomes a major second interval.
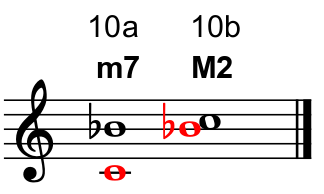
The distance between a C (the first note in a C major scale) and a Bb (the flatted seventh note) is a minor seventh (fig.10a).
When we raise the C an octave and place it above the Bb, e have inverted the interval and created a new one, measured from Bb to C (fig.10b).
The distance between a Bb (the first note in a Bb major scale) and a C (the second note) is a major second.
Fig.10
Inverted Diminished Intervals
Diminished Fourths
When we invert a diminished fourth interval, it becomes an augmented fifth interval.
The distance between a C (the first note in a C major scale) and an Fb (the flatted fourth note) is a diminished fourth (fig.11a).
When we raise the C an octave and place it above the Fb, we have inverted the interval and created a new one, measured from Fb to C (fig.11b).
The distance between an Fb (the first note in an Fb major scale) and a C (the sharped fifth note) is an augmented fifth.
Fig.11

Diminished Fifths
When we invert a diminished fifth interval, it becomes an augmented fourth interval.
The distance between a C (the first note in a C major scale) and a Gb (the flatted fifth note) is a diminished fifth (fig.12a).
When we raise the C an octave and place it above the Gb, we have inverted the interval and created a new one, measured from Gb to C (fig.12b).
The distance between a Gb (the first note in a Gb major scale) and a C (the sharped fourth note) is an augmented fourth.
Fig.12

Inverted Augmented Intervals
Augmented Fourths
When we invert an augmented fourth interval, it becomes a diminished fifth interval.
The distance between a C (the first note in a C major scale) and an F# (the sharped fourth note) is an augmented fourth (fig.13a).
When we raise the C an octave and place it above the F#, we have inverted the interval and created a new one, measured from F# to C (fig.13b).
The distance between an F# (the first note in an F# major scale) and a C (the flatted fifth note) is a diminished fifth.
Fig.13

Augmented Fifths
When we invert an augmented fifth interval, it becomes a diminished fourth interval.
The distance between a C (the first note in a C major scale) and a G# (the sharped fifth note) is an augmented fifth (fig.14a).
When we raise the C an octave and place it above the G#, we have inverted the interval and created a new one, measured from G# to C (fig.14b).
The distance between a G# (the first note in a G# major scale) and a C (the flatted fourth note) is a diminished fourth.
Fig.14

Complimentary Intervals
Any interval and its inversion are considered complimentary intervals.
The sum of an interval and its inversion always equals nine:
- An inverted second interval is a seventh interval.
- An inverted third interval is a sixth interval.
- An inverted fourth interval is a fifth interval.
- An inverted fifth interval is a fourth interval.
- An inverted sixth interval is a third interval.
- An inverted seventh interval is a second interval.
The quality of an inverted interval is the opposite of the quality of the original interval, except for perfect intervals, which remain perfect:
- An inverted major interval is a minor interval.
- An inverted minor interval is a major interval.
- An inverted diminished interval is an augmented interval.
- An inverted augmented interval is a diminished interval.
- An inverted perfect interval is a perfect interval.
Related Posts
Related posts include:
